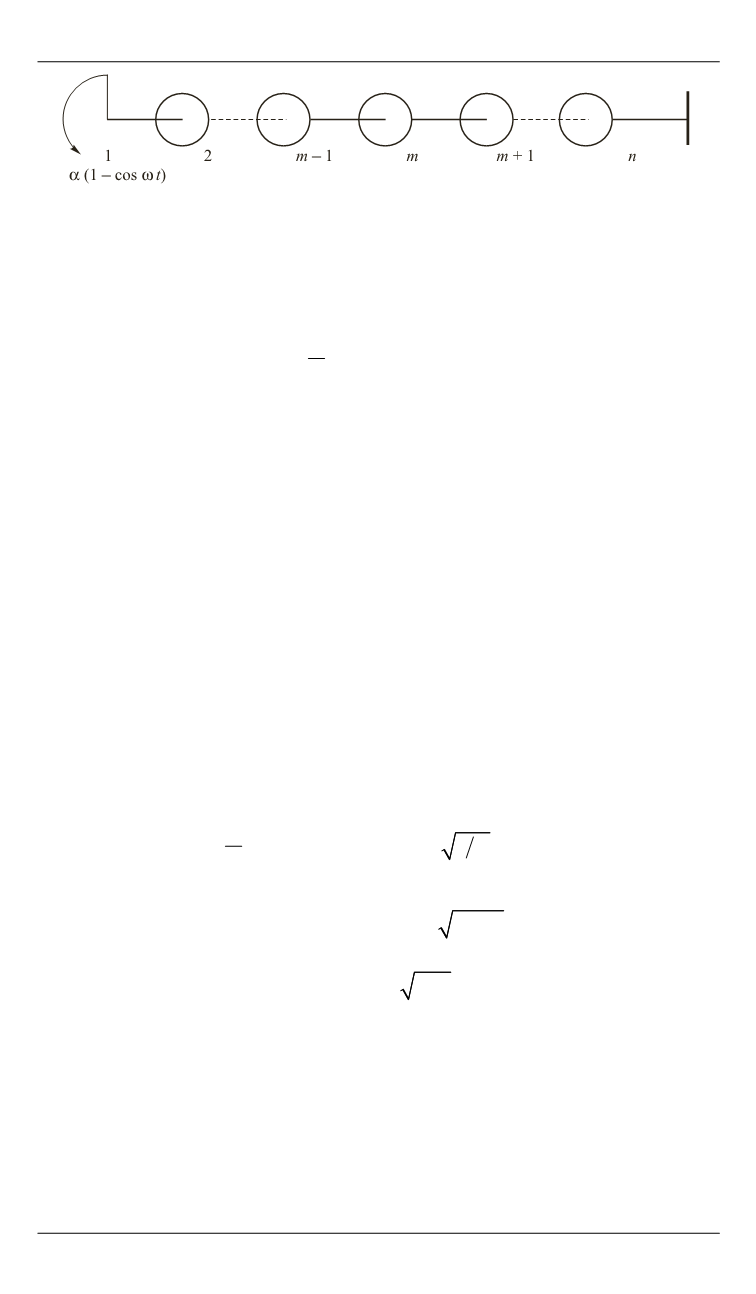
В.Ф. Смирнов, В.М. Зябликов
8
Рис. 2.
Однородная дискретная динамическая система
Дифференциальное уравнение движения
m
-го участка вал — диск
может служить разностным аналогом уравнения в частных производ-
ных, т. е. волнового уравнения
1
1
(
2
).
m
m
m m
c
J
+
−
ϕ = ϕ − ϕ + ϕ
(2)
Решение уравнения (2) отыскивается в виде бегущих волн, распро-
страняющихся от источника возмущения,
[
]
( , )
exp (
) ,
m
m t
A i t K
ϕ =
ω −
(3)
где
А
— комплексная амплитуда волны; ω — ее частота;
m
K
— фазо-
вая постоянная, зависящая от номера диска или участка (инерцион-
ная масса — жесткость)
m
.
В отличие от сплошной однородной среды фаза волны в этом
случае меняется не непрерывно, а скачком на величину
K
m
при пере-
ходе от (
m
– 1)-го к
m
-му диску (постоянная
K
m
является аналогом
волнового числа
K
=
2 / ,
π λ
где λ — длина волны, выраженная чис-
лом участков вал — диск системы).
Подставляя решение (3) в выражение (2), получаем дисперсион-
ное соотношение, свойственное однородным непрерывным системам
и связывающее частоту колебаний и волновое число
K
(а следова-
тельно, и длину волны),
2
2 (1 cos )
с
K
J
ω = −
или
[
]
2
sin( / 2) .
c J
K
ω =
(4)
Для возмущений, у которых sin
K
/ 2 ~
K
/ 2, из выражения (4)
следует линейный закон дисперсии
/
,
c JK
ω =
при котором гармо-
нические волны с разными частотами распространяются по системе с
одинаковой фазовой скоростью
ф
/ .
v
с J
=
В этом случае дискретная
динамическая система близка по своим свойствам к однородной си-
стеме, колебания которой описываются волновым уравнением.
Проанализируем поведение динамической системы, приведен-
ной на рис. 2, с учетом ее корпускулярных и волновых свойств. При
кинематическом возбуждении колебаний движение системы осу-
ществляется в соответствии с законом
1
(1 cos )
a
t
ϕ = − ω
первой без-
массовой точки при
0 2 /
t
≤ ≤ π ω
и
1
0
ϕ =
при
2 / .
t
≥ π ω