Н.В. Золотова, Р.С. Исмагилов
6
дим к третьей маркировке
''
. Продолжим в том же духе, пока это
возможно (т. е. пока имеются активные переходы), либо ограничимся
несколькими «тактами».
Итак, работа маркированной сети Петри есть (по определению)
цепочка
1 1
, ; ...
, ; ...
k k
t
t
(1)
(конечная или бесконечная) со следующими свойствами: 1)
k
— это
маркировки нашей сети, причем
1
— это исходная маркировка;
2)
t
k
— это переход, активный в маркировке
k
; 3)
k
+ 1
получается из
k
как результат запуска перехода
t
k
, т. е.
k
+ 1
= (
k
,
t
k
). Вот пример работы
сети Петри, изображенной на рис. 4 (ограничимся тремя тактами):
(100),
t
1
; (110),
t
2
; (021),
t
3
; (011).
4. Граф маркировок и дерево маркировок.
Возьмем сеть Петри
C
и рассмотрим следующий граф с мечеными ребрами. Каждая его
вершина — это некоторая маркировка сети; если
,
'
— две маркиров-
ки и
'
= (
,
t
k
), т. е.
'
получена из
запуском перехода
t
k
, то от
к
'
идет ребро с меткой
t
k
. Это и есть граф маркировок. Обозначим его
через
G
(
C
). Граф
G
(
C
) бесконечен (ибо бесконечно множество марки-
ровок).
Для каждой вершины графа
G
(
C
) (т. е. для каждой маркировки
)
обозначим через
G
(
C
,
) множество вершин, достижимых из
(по
путям в графе). Это есть связная, но, вообще говоря, не сильно связ-
ная компонента графа. Описание графа
G
(
C
,
) — он может оказать-
ся как конечным, так и бесконечным — это увлекательная и, как пра-
вило, достаточно сложная задача.
Перейдем к понятию дерева маркировок. Фиксируем маркировку
.
Для каждого активного в этой марки-
ровке перехода
t
k
изобразим ориенти-
рованное ребро (
,
'
), где
'
= (
,
t
k'
).
Пометим это ребро символом
t
k
. Та-
ким же образом поступаем с
'
. Про-
должая аналогичным образом, полу-
чаем дерево. Подчеркнем, что при
этом построении одна и та же марки-
ровка может встречаться более одного
раза. Получили дерево маркировок
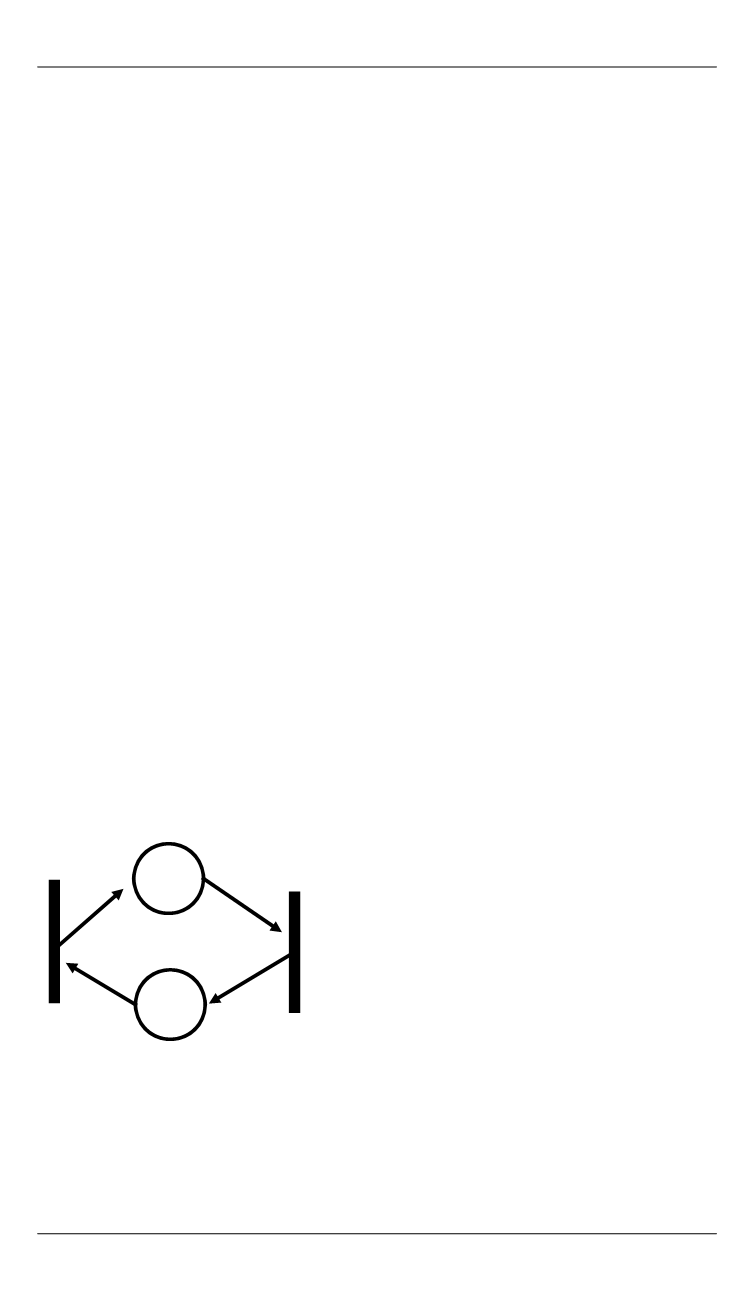
(рис. 11).
Пример 1.
Для сети
C
, изобра-
женной на рис. 11, дерево
T
(
C
,
) с начальной маркировкой
= (0, 1)
показано на рис. 12 (оно бесконечно). Граф
G
(
C
,
) устроен совсем
просто (рис. 13).
t
1
t
2
p
1
p
2
Рис. 11


